The Challenge

The goal is simple: place N chess queens on an N×N chessboard so that no two queens threaten each other. This challenge tests your strategic thinking and pattern recognition skills. As the board size increases, the puzzle becomes exponentially more difficult. For example, while an 8×8 board has 92 solutions, a 12×12 board has 14,200,000 solutions!

How to Use

1. Adjust the board size using the slider.
2. Click on a cell to place or remove a queen.
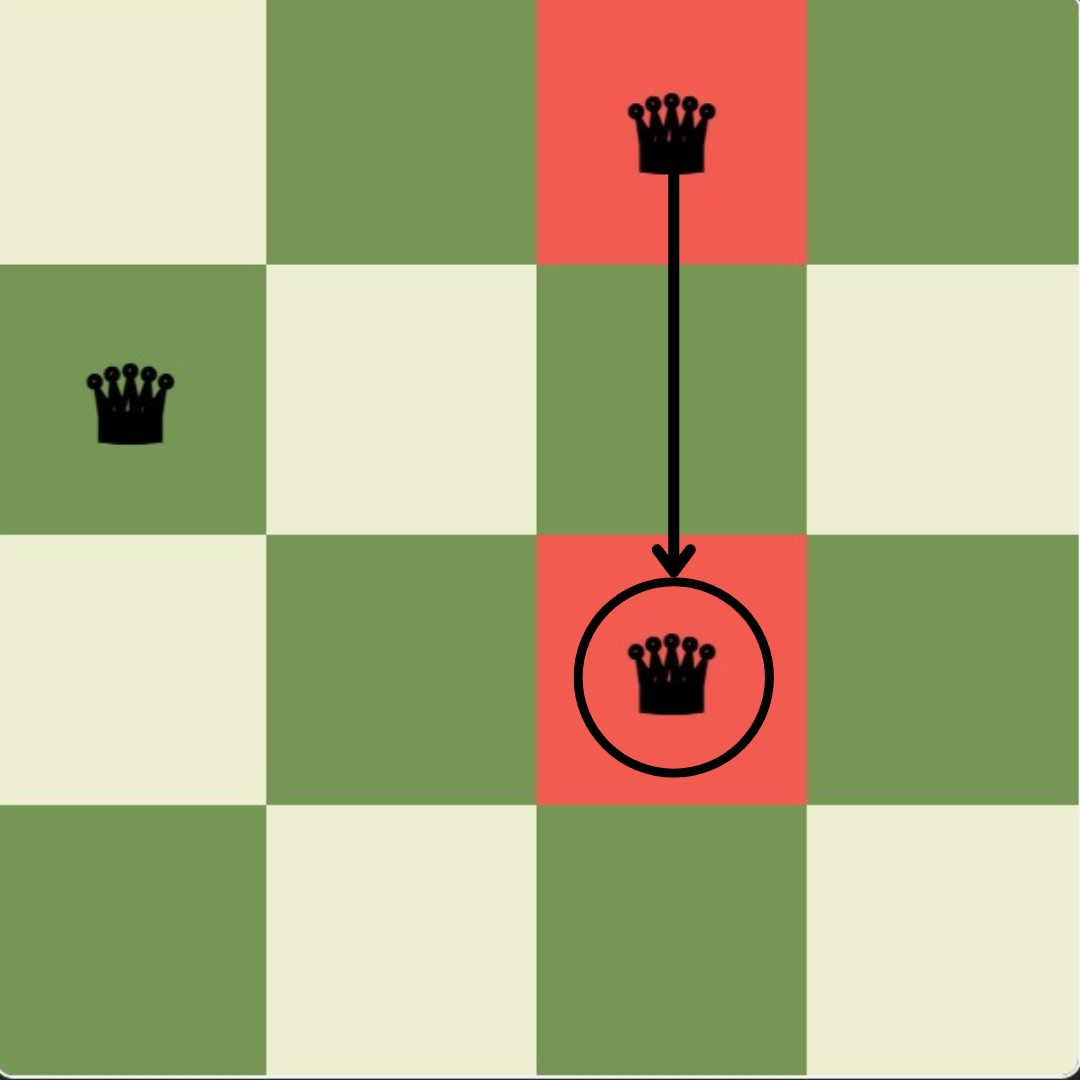
3. Unsafe queen positions will be highlighted in red.
4. Click Solve to find a solution automatically.
5. Use Reset to clear the board.
6. Toggle between themes with the theme button.

About the Problem

The N-Queen problem is a classic puzzle in computer science and mathematics. The challenge is to place N chess queens on an N×N chessboard so that no two queens threaten each other. In chess, a queen can attack any piece in the same row, column, or diagonal.

For a standard 8×8 chessboard, the goal is to place 8 queens safely. However, the problem can be generalized to any N×N board. As the board size increases, the number of possible arrangements grows exponentially, making it an excellent example of combinatorial complexity.

How to Solve

Using Backtracking Algorithm

Backtracking is an algorithmic technique for solving problems recursively by trying to build a solution incrementally, one piece at a time. If at any point it determines that the current solution cannot be completed, it "backtracks" to the previous step and tries a different path.

Start: Begin with an empty board.

Place: Try placing a queen in the first available position in the current row.

Check: If the placement is safe (no conflicts with other queens), move to the next row.

Recurse: Repeat steps 2-3 for the next row.

Backtrack: If a safe position can't be found, or if we've placed all queens successfully, backtrack to the previous row and try the next position.

Repeat: Continue this process until a solution is found or all possibilities are exhausted.

Why N-Queen Matters

The N-Queen problem is more than just a puzzle:

Algorithm Design: It's an excellent example for teaching recursive problem-solving and backtracking.

Optimization: Solving N-Queen efficiently requires optimizing the algorithm, making it a benchmark for algorithm performance.

Real-world Applications: The principles used in solving N-Queen apply to various real-world problems, including resource allocation, scheduling, and constraint satisfaction problems.

Complexity and Challenges

For an N×N board, there are N^N possible arrangements of queens. However, only a tiny fraction of these are solutions. As N increases, the problem becomes exponentially more difficult. The largest known solution has been found for N=27, requiring significant computational power.

About the Developer

Raunak Mandil

Hi, I'm Raunak, a passionate developer with a deep interest in algorithms and problem-solving. My journey with the N-Queens problem started in primary school when my cousin challenged me to place 8 queens on a chessboard without them threatening each other. That early fascination grew as I advanced in computer science, where I discovered the backtracking algorithm, which finally provided the solution to the puzzle that had intrigued me for years. This N-Queens Solver project is the result of that fascination, showcasing the elegance of backtracking and the complexity of combinatorial problems.

Beyond this project, I focus on developing software and web applications that solve complex problems. My skills range from algorithm design to UI/UX interfaces, and I particularly enjoy projects that combine logical challenges with visual elements, much like the N-Queens Solver. For more such projects, feel free to explore my website and GitHub.